• 关键词： 模型化 参数辨识 最小二乘法
• 摘要：对于一类具有自衡的非振荡的对象，把它近似成一阶惯性纯滞后环节。利用最小二乘参数估计方法，确定一阶惯性纯滞后环节传递函数参数。

1、引言

　　对于一个简单的系统，可以通过分析其过程的运动规律，应用一些已知的定理和原理，建立数学模型，即所谓的“白箱模型” 。但对于比较复杂的生产过程，该建模方法有很大的局限性。由于过程的输入输出信号总是可以测量的，而且过程的动态特性必然表现在这些输入输出数据中，那么就可以利用输入输出数据所提供的信息来建立过程的数学模型。这种建模方法称为系统辨识。把辨识建模称作“黑箱模型”。系统辨识又分为参数辨识和阶次辨识。本章只讨论参数辨识。

2、最小二乘辨识原理和应用

2.1最小二乘法原理

2.2最小二乘法的应用

最小二乘法的应用是十分广泛的，它又称曲线拟合。所以它可用来拟合各类曲线，如一元线性拟合、多项式拟合、指数函数拟合等。最小二乘法在控制理论方面的应用是比较多的，系统辨识中用的最多的就是最小二乘法辨识。最小二乘法原理简单，实现起来又较为方便，所以得到了广泛的应用。此外，最小二乘在统计学中也有一定程度的应用，在此就不再详述了。

3、模型辨识仿真研究

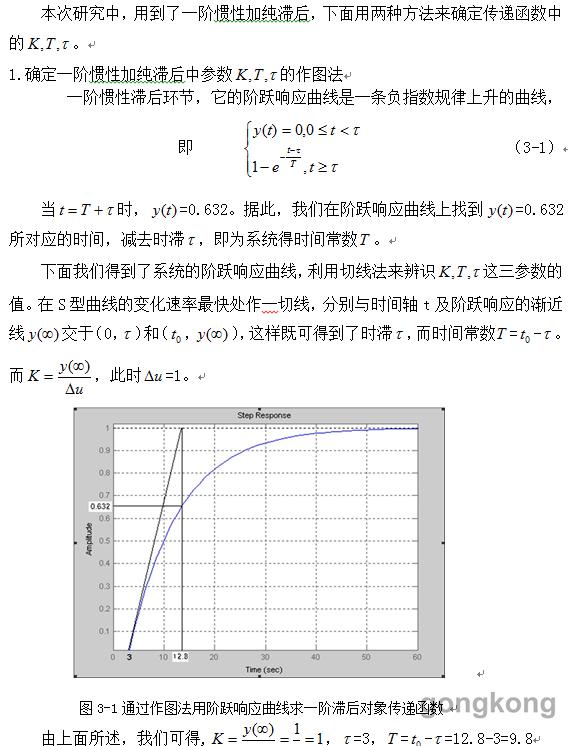
　　经典辨识法包括时域法、频域法和相关分析法。采用经典辨识法，直接获得的是非参数模型，一般是时间或频率为自变量的实验曲线或数据集。用阶跃函数、脉冲函数、正弦函数、或是随即函数作用于过程，直接得到的是阶跃响应、脉冲响应、频率特性、相关函数或谱密度，它们都是图形或数据集。对本类方法的对象，只需做出线性假定，并不需要事先确定模型的具体结构，因而本类方法适用范围广，工程上获得了广泛应用。

由图3-2可知，最小二乘辨识结果达到了很高的精度。此法抵抗过程量测噪声的鲁棒性强，不需要等待阶跃响应过程完全进入稳态，而且思路简单、清晰、易于编程。

4、小结

　　最小二乘是一种最基本的估计方法。它可用于动态系统，也可用于静态系统；可用于线性系统，也可用于非线性系统；可用于离线估计，也可用于在线估计。而且最小二乘这种算法有效地处理S型阶跃响应数据，自动辨识出滞后项，辨识的精确度明显提高。正因如此，在系统辨识和参数估计领域中，它获得了广泛的应用。

备注：本文为gongkong用户原创文章，未经作者本人或中国工控网授权，禁止转载！