【导读】马年到，小编在这里先祝贺大家马年吉祥，马上有钱，马上美丽，马上幸福！年前小编最后为大家介绍的是《开关变压器的分布电容工作原理及如何计算？》，马年之际，陶老师将继续为大家精心奉献开关变压器设计的相关专业知识——单激式开关电源的基本电路精讲！请大家尽请阅读！

马年到，小编在这里先祝贺大家马年吉祥，马上有钱，马上美丽，马上幸福！马年之际，陶老师将继续为大家精心奉献开关变压器设计的相关专业知识！请大家尽请阅读！

年前小编最后为大家介绍的是《开关变压器的分布电容工作原理及如何计算？》，接下来将奉献给大家的是“漏感与分布电容对输出波形的影响”的相关内容，该相关内容主要包括五个大的方面：1、单激式开关电源的基本电路；2、对漏感与分布电容的影响进行数学分析；3、电源开关管的过压保护电路；4、电源开关管保护电路参数的计算；5、RCD尖峰脉冲吸收电路参数计算举例。这里先为大家介绍第一个方面：单激式开关电源的基本电路。其他的将会在后面一一奉献！请大家关注本站更新！

1．单激式开关电源的基本电路

图1是单激式开关电源的基本原理图。图中，T为开关变压器，N1和N2分别为开关变压器初、次级线圈；Ls为开关变压器的漏感， Lu为开关变压器初级线圈的励磁电感；Cs为开关变压器初级线圈的分布电容，RL为开关变压器次级线圈的输出负载，Q1为电源开关管。

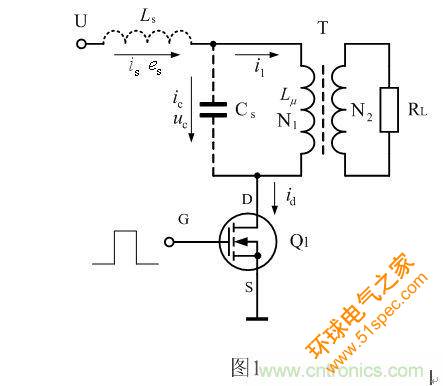
变压器初级线圈或次级线圈的分布电容Cs可按下式进行计算：

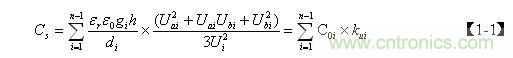
式中， 为第 i层与i +1层线圈之间的静态电容， i = 1、2、3、? ? ?、n ，n为所求总分布电容的变压器初级线圈或次级线圈的层数； gi为第i 层与 i+1层线圈之间的平均周长； Kui为第i 层与i +1层线圈之间分布电容的动态系数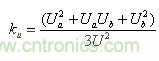， ，它与加到电容两端的电压有关，ku 是一个小于1的系数；

 Ui为第 i层与i +1层线圈之间的标准电位差，其值一般等于相邻两层线圈工作电压之和，即： ，U为变压器初级线圈或次级线圈两端的工作电压；Uai 、Ubi 分别为第 i层与i +1层线圈之间X=0 和 X=h处对应的电位差；当线圈层间按S绕法时， Uai = 0，Ubi  =  Ui；当线圈层间按Z绕法时，  Uai =Ubi  =  1/2Ui。

如果不考虑变压器次级线圈对初级线圈的影响，对于一个功率大约为100瓦的开关变压器，其初级线圈的分布电容大约在100~2000微微法之间；如果把次级线圈的分别电容也考虑进去，总的分布电容可能要大一倍左右，因为初、次级线圈分布电容的转换比是平方的关系。因此，分布电容对输出波形的影响是很大的。关于开关变压器的分布电容的计算，请参看《2-1-21．开关变压器的分布电容》章节的内容。
[page]

根据变压器的工作原理，图1中的开关变压器还可以等效为图2所示电路。

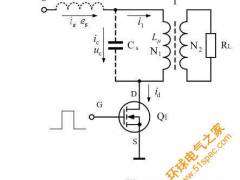
在图2中，Ls为漏感，漏感也称漏磁电感，或称分布电感；Cs为分布电容（总分布电容）， Lu为励磁电感，R为等效负载电阻。设开关变压器初级线圈的电感为L，则L=Ls+Lu ；而分布电容Cs，则包括次级线圈等效到初级线圈一侧的分布电容，即，次级线圈的分布电容也要等效到初级线圈回路中；同理，等效负载电阻R，就是次级线圈的负载RL被等效到初级线圈回路中的电阻。

设次级线圈的分布电容为C2，等效到初级线圈后的分布电容为C1，则有下面关系式：

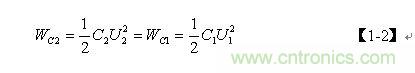
上式中， Wc2为次级线圈分布电容C2存储的能量， Wc1为C2等效到初级线圈后的分布电容C1存储的能量；U1、U2分别为初、次级线圈的电压，U2 = nU1，n = N2/N1为变压比，N1 、N2分别为初、次级线圈的匝数。由此可以求得C1为：

【1-2】和【1-3】式的计算方法不但可以用于对初、次级线圈分布电容等效电路的换算，同样可以用于对初、次级线圈电路中其它电容等效电路的换算，以及用于对负载电阻的换算。所以，C2亦可以是次级线圈电路中的任意电容，C1为C2等效到初级线圈电路中的电容。

由此可以求得图2-44中，变压器的总分布电容Cs为：

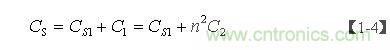
【1-4】式中，Cs为变压器的总分布电容，Cs1为变压器初级线圈的分布电容；而C1为次级线圈电路中所有电容等效到初级线圈电路中的电容；C2为次级线圈电路中所有电容（包括分布电容与电路中的电容）；n = N2/N1为变压比。

虽然看起来，图2-44开关变压器的等效电路与一般变压器的等效电路没有根本的区别，但开关变压器的等效电路一般是不能用稳态电路进行分析的；即：图2-44中的等效负载电阻R不是一个固定参数，它会随着开关电源的工作状态不断改变。例如，在反激式开关电源中，当开关管导通时，开关变压器是没有功率输出的，即负载电阻R等于无限大；而对于正激式开关电源，当开关管导通时，开关变压器是有功率输出的，即负载电阻R既不等于无限大，也不等于0 。因此，分布电感与分布电容对正激式开关电源和反激式开关电源工作的影响是不一样的。

图3是开关变压器与电源开关管连接时的工作原理图。图3中，Q1为开关管，Cds为开关管漏极和源极之间的分布电容，Cgs为开关管栅极和源极之间的分布电容。值得说明的是，这里的Cgs和Cds都不是一个单纯性质的电容，它只是在开关管的导通和关断的一瞬间，其阻抗的变化过程与电容（或电感）的充放电过程很类似；而它的基本性质实际上还是属于电阻，因为它会损耗功率。
[page]

当开关管开始导通时，外电路给栅极（绝缘栅场效应管）加一正电压，通过静电感应，开关管耗尽层中的载流子（电子）在电场的作用下会重新进行分布，耗尽层中载流子浓度按指数规律不断增加，这个过程相当于对电容Cgs进行充电；随着耗尽层中载流子的重新分布，耗尽层的厚度也相应增加，其结果是耗尽层的电阻由大变小。

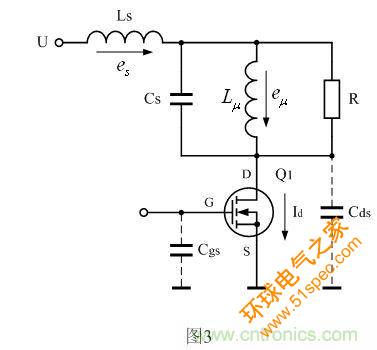
因此，当开关管刚开始导通时，流过开关管的电流是由小变大，这个过程，与在电感两端加一电压方波时，流过电感的电流由小变大很相似；所以，在开关管刚导通的一瞬间，开关管的漏极和源极之间可以等效成一个电感Lds。由于这个电感相对分布电感Ls和励磁电感Lu 来说很小，所以图3中没有画出。

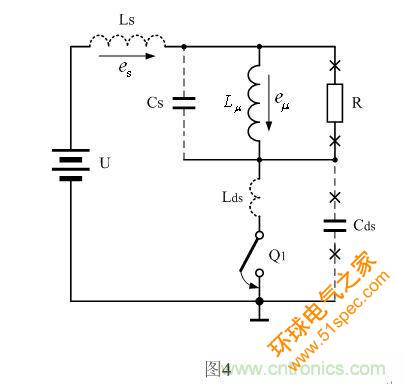
图4是图3中的开关管Q1导通时对应的等效工作原理图。在图4中，电感Lds为开关管Q1导通时的等效电感，当开关管Q1导通时，开关管的内部电阻将随时间由大逐步变小，它的作用好像一个电感，因此，当开关管Q1导通时，开关管可以等效成一个理想的开关与一个电感串联。但这个电感属于电阻性质，它会损耗能量，它不像实际中的电感那样可以储存能量（磁能），它实际上属于一个阻值由大变小的可变电阻，但如果用一个可变电阻来表示，在计算过程中将会很复杂，并且在开关管Q1导通的变化过程中，用一个可变电阻来表示也没有用一个电感来表示显得形象。

当开关管开始关断时，外电路给栅极加一负电压（或低电压），通过静电感应，开关管内耗尽层中的载流子（电子）在电场的作用下会重新进行分布，相当于外电路要向耗尽层抽离载流子，耗尽层中载流子的浓度将按指数规律减小，耗尽层的厚度也将随时间增大而变小，其结果是耗尽层的电阻将随时间由小变大。这个过程，与电容被充电时，流过电容的电流由大变小很相似；所以，当开关管刚导通的一瞬间，开关管可以等效成一个理想的开关与一个电容器并联，这个电容器就是漏极和源极之间的分布电容Cds。图5是开关管关断时，反激式开关电源的工作原理图。

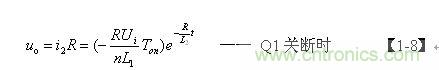
根据上面分析，栅极电容Cgs对开关管的导通影响比较大，容量越大，开关管的导通上升时间就越长。而漏极电容Cds对开关管的关断影响比较大，容量越大，开关管关断存储时间就越长。电容Cgs和Cds也称扩散电容，它们既具有电阻的性质，同时也具有电容充放电的特性，这种特性主要与耗尽层中载流子的浓度变化有关。
[page]

当电源开关管为晶体管时，Cgs和Cds分别与Cbe和Cce对应，工作原理场效应管的工作原理基本相同或相似。不过基区参与导电的载流子的密度的增加或减少，不是靠静电感应的作用，而是靠基极电流的注入。

由于开关管在导通或关断期间，其分布参数的性质和作用也在改变，因此，在图2-43～图5中，要对分布电感Ls和分布电容Cs，以及Cgs和Cds组成的电流回路进行精确计算，难度是很大的。下面，我们将以很长的篇幅来对上面电路进行分析和计算。

在图4中，分布电感Ls和分布电容Cs可以看成是一个串联振荡回路，当开关管Q1开始导通的时候，输入脉冲电压的上升率远远大于输入电压通过分布电感Ls对分布电容Cs充电电压的上升率，此时，串联振荡回路开始吸收能量，输入电压通过Lds和Ls对Cs进行充电，流过Ls和Cs的电流按正弦曲线增长；当开关管Q1完全导通以后，Lds的值等于0，此时，输入脉冲进入平顶阶段，相当于输入脉冲电压的上升率为0，由于，输入脉冲电压的上升率远远小于分布电感Ls与分布电容Cs进行充、放电时电压的上升率，因此，振荡回路开始释放能量，振荡回路会产生阻尼振荡。

由于分布电感Ls和分布电容Cs的时间常数相对于励磁电感 Lu比较小，所以分布电感Ls和分布电容Cs产生阻尼振荡的过程主要发生在开关管Q1导通和关断的一瞬间。当开关管Q1导通或关断后不久，阻尼振荡很快就会停止。当输入电压对分布电容Cs充满电后，输入电压就完全加到励磁电感Lu 的两端。如果是反激式开关电源，流过励磁电感 Lu的电流将随时间从0开始线性增加；如果是正激式开关电源，流过励磁电感 的电流将随时间按梯形波曲线增长。

在开关管Q1导通期间，由于开关管的导通内阻非常小，分布电容Cds基本上是不起作用的。当开关管Q1由导通状态转换为关断时，开关管漏极和源极之间的分布电容Cds将被接入电路中，分布电感Ls和励磁电感Lu 将同时产生反电动势，并分别对分布电容Cds和Cs进行充、放电，电容与电感在交替进行能量交换的过程中，将产生串、并联振荡。

但由于励磁电感Lu  的时间常数比Ls、Cs和Cds的时间常数大好多，因此，在产生振荡的过程中，主要由Ls、Cs和Cds三者产生作用。另外，在开关管开始关断期间，由于Cds实际上是一个阻抗由小到大，其阻抗变化过程类似于电容充电的可变电阻，它只吸收能量，而不会释放能量。因此，它在产生振荡的过程中，只对充电曲线的上升速率起影响，而对放电曲线的下降速率不起影响。

图6是图4和图5电路中，当开关管导通时（图4），输入电压ui通过开关变压器漏感Ls对分布电容Cs进行充电，使漏感Ls与分布电容Cs产生冲击振荡时，分布电容Cs两端的电压波形；和当开关管关断时（图5），输入电压ui与开关变压器漏感Ls和分布电容Cs、Cds产生充、放电时，电源开关管D、S极两端的波形。

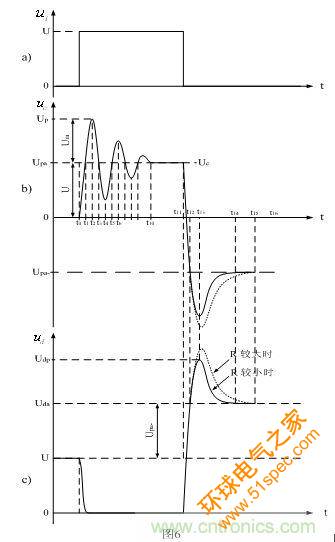
在图6中，图6-a是电源开关管Q1导通时，输入电压ui加于开关变压器初级线圈两端的电压波形；图6-b是分布电容Cs两端的电压波形；图6-c，是电源开关管Q1漏极D与源极S之间的电压波形。

在t0时刻，电源开关管Q1开始导通，输入电压ui加于开关变压器两端，输入电压ui首先通过分布电感Ls对分布电容Cs充电，此时，由于输入电压ui的上升率大于电流通过分布电感Ls对分布电容Cs进行充电的电压上升率，所以，分布电感和分布电容都从输入电压吸收能量。输入电压ui在对分布电感Ls和分布电容Cs进行充电过程中，分布电容Cs两端的电压是按正弦曲线上升的；而放电时，其两端的电压则按余弦曲线下降。

到t1时刻，流过Ls的电流达到最大值，同时分布电容Cs两端的电压与输入电压ui相等（或与变压器初级线圈的正激输出半波平均值Upa相等），此时输入电压ui的上升率为0，输入电压ui的上升率小于分布电感Ls对分布电容Cs充电的电压uc上升率，所以，分布电感Ls开始释放能量继续对分布电容Cs进行充电。此时，Ls在释放能量，而输入电压ui和分布电容Cs都在吸收能量，分布电容Cs都两端的电压uc继续按正弦曲线上升。

到t2时刻，流过Ls的电流等于0（储存于Ls中的能量被释放完毕），分布电感产生的反电动势对分布电容Cs进行充电结束，此时Cs两端的电压也达到最大值，然后Cs开始按余弦曲线对Ls和输入电压ui进行放电，流过Ls的电流开始反向，Ls开始反向储存磁能量。

到t3时刻，Cs两端的电压又与输入电压ui相等，电容停止放电，此时，Ls储存的磁能量将转化成反电动势es给电容Cs进行反向充电，使Cs两端的电压低于输入电压ui 。

到t4时刻，流过Ls的反向电流等于0，Cs两端的电压达到最低值，然后输入电压又开始通过Ls对Cs进行充电，至此，分布电感Ls与分布电容Cs第一个充放电周期结束。
[page]

到t4时刻之后，输入电压ui对分布电感Ls和分布电容Cs进行充电的过程，以及分布电感Ls和分布电容Cs互相进行充电的过程，与t0～t4时刻基本相同。但由于在此期间，输入电压的上升率等于0，输入电压不再向分布电感Ls和分布电容Cs提供能量，因此，分布电感Ls与分布电容Cs产生自由振荡的幅度是随着时间衰减的，其衰减速率与等效电阻大小有关。

到t10时刻，分布电感Ls与分布电容Cs产生的阻尼自由振荡的幅度被衰减到差不多等于0，此时，分布电容Cs两端的电压等于变压器初级线圈的正激输出半波平均值Upa。关于半波平均值Upa和Upa-的计算方法及定义，请参考第一章的（1-70）和（1-71）式及说明。

在图6-b中，Upa为变压器初级线圈正激输出电压的半波平均值，此值与输入电压相等；Upa-为变压器初级线圈反激输出电压的半波平均值，此值与占空比相关；当占空比等于0.5时，Upa-与输入电压在数值上相等，但符号相反。

到t11时刻，电源开关管Q1开始关断，由于流过分布电感Ls和励磁电感Lu的电流通路突然被切断，其必然会产生反电动势Es 和Eu，此二反电动势将与输入电压ui一起串联对分布电容Cs和Cds进行充电。但由于Cs两端的电压与 Eu电压基本相等，因此，对分布电容Cds进行充电的电压正好是输入电压ui与反电动势电压Es和Eu三者之和。

到t12时刻，电源开关管Q1已经完全关断，但二反电动势Es和Eu 与输入电压ui还继续对分布电容Cs和Cds进行充电，不过，此时Cds的容量已经变得非常小，因为它表示开关管内部的扩散电容，属于电阻性质，当开关管完全关断之后，阻值为无限大。

直到t13时刻，分布电感Ls储存的磁能量基本被释放完，二反电动势Es 和 Eu才停止对分布电容Cs和Cds继续进行充电；此时，分布电容Cs和分布电容Cds的两端电压均达到了最大值，即，加到电源开关管Q1漏极上的电压达到最大值；而后，分布电容Cs又对原充电回路进行放电，并产生自由振荡，但由于电源开关管Q1关断后阻抗为无效大，其放电回路只能通过等效R和励磁电感 进行，所以振幅很快就衰减到0。图6-c为电源开关管D、S两端的波形。

在图6-c中，Uda为开关管Q1关断期间，D、S两极之间电压的半波平均值，Uda等于输入电压ui（ui=U）与变压器初级线圈产生反激输出电压的半波平均值Upa-之和；Udp为开关管关断期间D、S两极之间电压的峰值。Udp和Uda的值均与占空比有关，当占空比等于0.5时，Uda约等于输入电压ui（ui=U）的2倍，而Udp则大于输入电压的2倍，并且Udp的值还与漏感Ls的值大小有关，Ls的值越大，Udp的值也越大。

开关变压器次级线圈输出电压的半波平均值Upa和Upa-由下面两式求得：

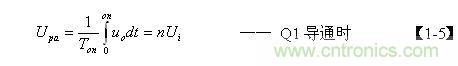
【1-5】式中的uo为正激输出电压，其值为：

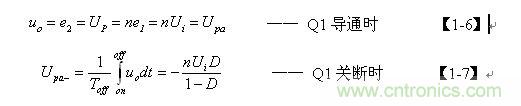
【1-7】式中，D为占空比，uo为反激输出电压，其值为：

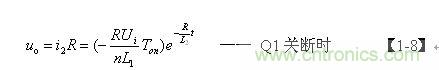
【1-8】式中，L1、L2分别为开关变压器初、次级线圈的电感，n为开关变压器线圈的匝数比，n=N2/N1，Ui为变压器初级线圈的输入电压，Ton为开关管的导通时间，R为等效负载电阻。

值得说明的是，上面【1-5】～【1-8】式并没有把分布电感Ls对输出电压的影响考虑在其中。

由于分布电容Cds表示开关管内部的扩散电容，它的容量在Q1的关断过程中一直在改变（由大变小），因此，分布电感Ls和励磁电感 产生的反电动势 和 对分布电容Cds进行充电时，其电压上升率并不是完全按正弦曲线规律变化。另外，由于励磁电感Lu在数值上远比分布电感Ls大，因此， Lu和Cs产生自由振荡的频率比Ls和Cs产生自由振荡的频率低很多。

这里顺便指出，图6-b的波形是很难测量到的，因为分布电感Ls与分布电容Cs产生自由振荡的过程，基本上都在变压器内部的分布电感与分布电容之间进行，用仪器很难直接进行测量；但通过测量变压器次级线圈的波形，也可以间接测量图6-b中波形的振幅；而图6-c的波形可以直接进行测量，两者的振幅均与分布电感Ls的数值大小有关，还与等效电阻R的阻值有关。分布电感Ls的数值越大，振幅也越大，等效电阻R的阻值越大，振幅也越大。

当自由振荡很强时，自由振荡会通过电磁辐的形式给周边的电路或电子设备造成EMI干扰。这一点在进行开关变压器设计时务必要注意，应该尽量减小分布电感Ls的数值。

下面我们进一步通过数学的计算方法来对电路的参数进行详细分析。请大家密切关注下次更新：《对漏感与分布电容的影响进行数学分析》

【连载】陶显芳老师谈开关变压器的工作原理与设计：

线圈电感量的计算及几种典型电感介绍
http://www.cntronics.com/power-art/80022174
开关变压器的漏感工作原理及计算
http://www.cntronics.com/power-art/80022173
开关变压器铁芯脉冲导磁率与平均导磁率的测量
http://www.cntronics.com/power-art/80022172
双激式开关变压器铁芯磁滞损耗、涡流损耗的测量
http://www.cntronics.com/power-art/80022171
单激式开关变压器铁芯磁滞损耗、涡流损耗的测量
http://www.cntronics.com/power-art/80022170
开关变压器涡流损耗分析及铁芯气隙的选取
http://www.cntronics.com/power-art/80022166
开关变压器磁滞损耗分析及铁芯磁滞回线测量
http://www.cntronics.com/power-art/80022164
双激式的相关参数计算以及设计时存在的风险评估
http://www.cntronics.com/power-art/80022163
开关变压器铁芯导磁率及初始化曲线介绍
http://www.cntronics.com/power-art/80022154
开关变压器的工作原理及脉冲对铁芯的磁化
http://www.cntronics.com/power-art/80022153