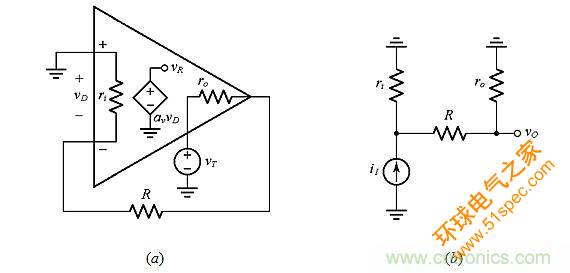
【导读】负反馈电路分析最常见的方法是双端口分析（TPA）和回归比（RRA）分析。两者既有不同，也有相似，常让人困惑，本设计实例用大家熟悉的电路实例深入阐述这两种技术。在图1的两个框图中，使用下标TP和RR来区分双端口和回归比这两种类型。

具体而言，α_TP和α_RR是开环增益，而?_TP和?_RR是反馈系数。图1a假设是单向块，图1b则更通用，因为它还考虑了误差放大器周围的馈通（feedthrough），如增益块α_ft所表示的。

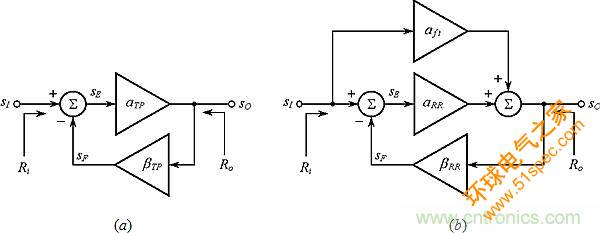
图1：（a）双端口（TP）和（b）回归比（RR）分析的负反馈框图。

双端口分析（TPA）

取决于s_I和s_O是电压还是电流，有四种可能的拓扑结构，如图2中的运放所示。在每个分图题中，连字符前面的一项是指输入相加的方式（串联电压，并联电流），而连字符后面的一项是指反馈网络采样s_O以产生反馈信号s_F的方式（并联电压，串联电流）。对每个拓扑结构，闭环增益呈现形式为：

其中：

是环路增益，A_ideal是极限条件（T_TP→ ∞）中s_O/s_I的值，通过使α_TP→ ∞得到。另外，反馈系数是：

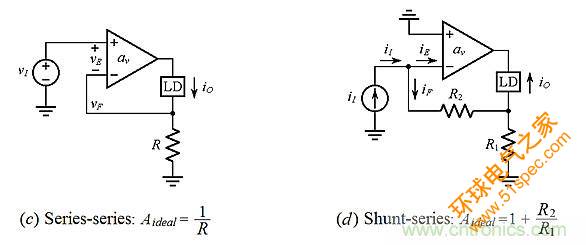
图2：使用运放来说明四种基本反馈拓扑。

TPA寻求一种会考虑放大器和反馈网络之间任何交互（如加载）的α_TP表达式。负反馈将每个端口的开环电阻r_pa转换为闭环电阻，使这项任务变得容易：

8

串联情况下为+1，并联情况下为-1。如果T_TP 足够大，在串联情况下可将R视为开路，在并联情况下可将其视为短路。

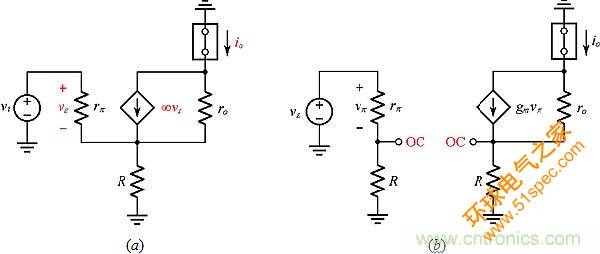
作为第一个例子，我们将TPA应用到图3a的电流放大器，该电路有：

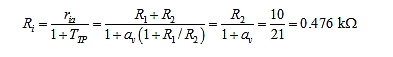
为得到α_TP，我们修改了误差放大器，如图3b所示。图3a中输入源看到的电阻是R_i= R₂/(1 + α_v)，负载看到的电阻是R_o = R₁(1 + α_v)。对于大的α_v，我们期望R_i很小、R_o很大。因此，如果我们将R_o近似为开路（OC），那么从放大器的输入端口看到的反馈网络就是R₂ + R₁的简单串联组合。同样，如果我们

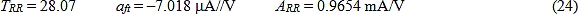
图3：（a）端接于短路负载的并联-串联配置；（b）使用TPA查找开环参数α_TP、r_ia,和r_oa的电路。

将R_i近似为短路（SC），则从放大器输出端口看到的反馈网络就是R₂//R₁的简单并联组合。因此我们有：

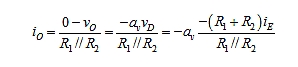
表明开环增益为：

注意，α_TP ≠ α_v。简化后的循环增益：

重新考虑α_v = 10 V/V和R₁ = R₂ = 10kΩ的例子。带入上面的等式，给出：

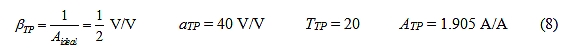
尽管有OC和SC近似值，但通过与直接分析得出的 A_exact = 1.909 A/A相比，这相当有利。为确保这种近似性不是偶然的，我们来检查R_i和R_o的值。通过检查图3b，我们有r_ia=R₂+R₁和r_oa=R₂//R₁。应用等式（4），我们得到：

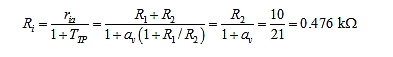
从而证实R_i比电路中的其它电阻小得多，R_o大得多。

回归比分析（RRA）

这种方法，如图1b的块图所示，可计算闭环增益：

其中，T_RR是环路增益，A_ideal 和α_ft分别是T_RR → ∞和T_RR→ 0极限条件下s_O/s_I的值。这些极限是通过使图1b中的α_RR → ∞ 和α_RR → 0来实现。根据以下流程，得到T_RR为误差放大器的从属源α_RRs_E的回归比：

（a）设置s_I → 0； （b）在从属源α_RRs_E的紧下游立即切断反馈环； （c）与α_RRs_E源相同类型和极性的测试信号s_T通过电路下游； （d）找到由从属源本身返回的信号s_R； （e）获得回路增益作为回归比。

随着分析的进行，我们发现将TRR表达为积很方便，类似于公式（2）：

得到反馈系数β_RR：

或更简单地，β_RR=T_RR/α_RR。

将这个过程应用于图3a的电流放大器，产生了图4a的电路，通过检查，我们有v_R = α_vv_D = α_v(–v_T)，所以：

因此，α_RR = α_v和β_RR = T_RR/α_RR = 1。使α_v → 0，以便得到馈通增益，如图4b所示。通过检查，i_O = i_I，所以，α_ft= i_O/i_I = 1 A/A。再考虑α_v = 10V/V和R₁= R₂ = 10kΩ的例子，我们现在有：

对比公式（14）与公式（8），观察各个T、α和β值的不同。另外，A_RR是准确的，而A_TP只是近似。为了符合图1a中采用单向块这一假定，TPA通过使T_TP = 20（与T_RR = 10相比）尽可能地接近A_exact。对于α_v的当前值来说，使T_TP = 21（而非20）将导致A_TP = A_exact，这可以很容易验证。但是，对于馈通变得更相关的较低值（例如α_v=1V/V）来说，它不起作用。 α_v = 0时，差异最大，其中，A_RR=A_exact=1 V/V，但A_TP = 0。

图4：用于得到图3a中电流放大器的（a）环路增益T_RR和（b）馈通增益α_ft的电路。

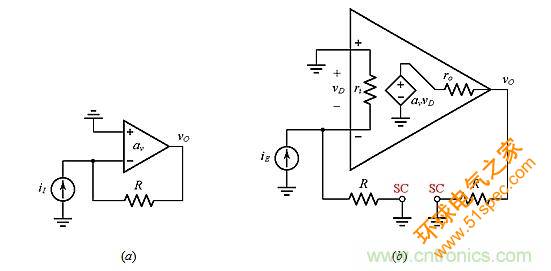
图5：（a）并联-并联配置；（b）得到误差增益α_TP的电路。

更复杂的例子

我们将这两种方法应用于图5a的I-V转换器，但是使用具有非无限输入阻抗r_i和非零输出阻抗r_o的更真实的运放模型。正如我们知道的，该电路有：

由于这是一个并联-并联拓扑结构，所以反馈电阻同时为输入和输出两个端口的接地电阻，如图5b所示。我们有：

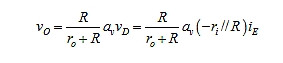
表明开环增益：

再次注意α_TP ≠α_v。而且，环路增益为：

对于RRA，请参考图6的电路，它分别给出：

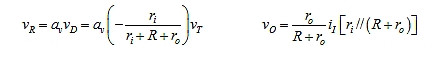
所以环路和馈通增益简化为：

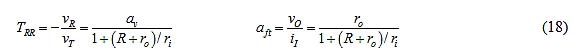
注意，α_ft和A_ideal极性相反。我们针对一种容易想象的特定情况，即α_v = 60 V/V和r_i= r_o = R = 10kΩ，来比较这两种方法。是的，用一款不太合格的运放，可以更好地显示其差异。把这些数据带入相关公式，得到：

图6：用于得到图5a中I-V转换器的（a）环路增益T_RR和（b）馈通增益α_ft的电路。

注意α_TP和α_RR以及β_TP和β_RR的幅值、极性和量纲的差别。A_TP 和A_RR (=A_exact)也有细微差别。

如果运放r_o = 0，根据公式（18）将不存在馈通。在这种情况下，我们将得到：T_TP = T_RR = 30，A_TP = A_RR = –9.677V/mA。如果运放也有r_i = ∞，则T_TP = T_RR = 60，A_TP = A_RR = –9.836 V/mA。然而，仍然会有很大的差异，即α_TP = –600 V/mA和β_TP = ?0.1 mA/V，以及α_RR = 60 V/V 和β_RR = 1。尽管存在差异，这两个参数集仍将设法提供相同的A值！

另外两个例子

最后我们来看一看图7a和b的单晶体管电路。图7c中其共同小信号模型表明，误差增益基于g_m（在运放的盒子中，它是基于α_v的）。而且，两个电路都是串联-输入型的。然而，根据我们将输出作为发射极电压v_o还是作为集电极电流i_o，分别有并联-输出或串联-输出类型。两个电路都很简单，可以直接分析它们。但是，通过TPA和RRA进行研究将更具启发性。

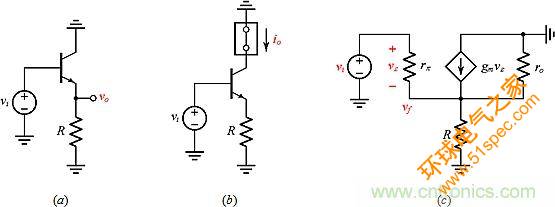
图7：假定g_m = 40mA/V，r_π = 2.5kΩ，r_o = 40kΩ和R = 1.0kΩ。（a）串联-并联电路；（b）串联-串联电路；（c）其共同的小信号模型。

● 图7a串联-并联电路的TPA：为得到A_ideal，让g_m → ∞，如图8a所示。这使得v_ε→ 0或v_o → v_i，意味着A_ideal = 1.0V/V (= 1/β_TP)。参照图8b，通过检查，我们有v_o=g_m(R//r_o)v_ε或α_TP=v_o/v_ε=g_m(R//r_o)。带入数据，可以得到：

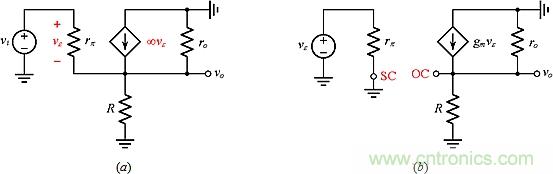
图8：用于得到图7a中串联-并联电路的（a）A_ideal和（b）α_TP的电路。

● 图7a串联-并联电路的RRA：为得到T_RR，参见图9a，其中i_r = g_mv_π = g_m[(-i_t)(r_π//R//r_o)]；为得到α_ft，参见图9b，其中v_o = v_i(R//r_o)/[r_π + (R//r_o)]。所以：

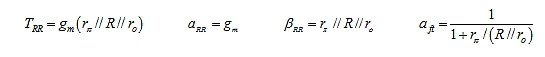
带入数据，得到：

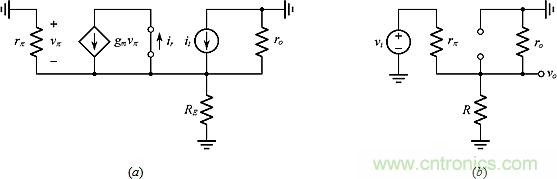
图9：用于得到图7a中串联-并联电路的（a）T_RR和（b）α_ft的电路。

● 图7b串联-串联电路的TPA：为得找A_ideal，让g_m → ∞，如图10a所示。这使得v_ε→ 0，从而在r_π上产生虚拟短路，所以i_R = v_i/R。超级节点处的KCL给出i_o = i_R = v_i/R，所以A_ideal=i_o/v_i=1/R(=1/β_TP)。要得到α_TP，按图10b继续。结果如下：

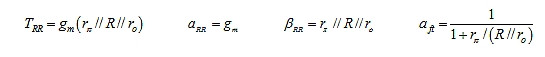
带入数据，得出：

图10：用于得到图7b中串联-串联电路的（a）T_RR和（b）α_ft的电路。

● 图7b串联-串联电路的RRA：为得出T_RR，参见图11a。 这与图9a相同，所以我们有相同的T_RR。要得到α_ft，按图11b继续。结果如下：

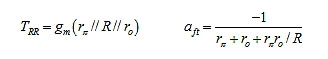
带入数据，得出：

串联-串联电路的馈通比串联-并联电路的小，所以A_TP →A_RR。

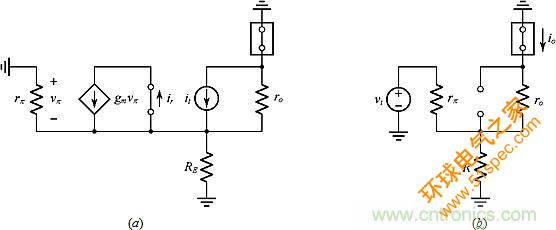
图11：用于得到图7b中串联-串联电路的（a）T_RR和（b）α_ft的电路。

比较TPA和RRA

前面利用以运放和晶体管作为增益元件（运放的增益为α_v，晶体管的为g_m）的简单电路，讨论了所有四种反馈拓扑结构。比较过程和结果，我们发现：

• RRA比TPA更通用，因为它考虑了误差放大器周围的馈通。因此，RRA的结果是准确的，而TPA的结果只是近似。

• 对于高环路增益，TPA和RRA之间的差别最小，当环路增益下降到零时，差别最大，其中A_RR→α_ft但A_TP→0。

• TPA将环路增益计算为乘积TTP = α_TPβ_TP；RRA将其计算为比值T_RR = –v_R/v_T。

• TPA对四种反馈拓扑中的每一种都使用了不同的双端口表述，所以一般情况下，不同拓扑结构的α_TP、β_TP和T_TP会不同。

• 相比之下，给定电路的环路增益T_RR与拓扑结构无关，而是取决于输入和输出信号的类型和位置（但α_ft通常与拓扑结构相关）。

• 对于误差放大器和反馈网络之间的任何交互（如加载），两种分析的处理方式都不同。TPA假定β_TP = 1/A_ideal，然后通过使用OC和SC近似来操控放大器电路以得到α_TP，所以通常α_TP≠α_v(或α_TP≠g_m)。

• 除打破信号注入环路之外，RRA不会影响电路的操作。 RRA假定了α_RR = α_v (或α_RR = g_m)，它将误差放大器和反馈网络间相互作用的影响转移到反馈网络本身，所以通常β_RR≠1/A_ideal。

• TTP和TRR有时可能相同，但不应该把这当作常态。尤其不应该使用T_RR来计算A_TP，或使用T_TP计算A_RR。例如，在尝试使用公式（3）时发生的错误。

• RRA感觉更直观，也更适合实验室的计算机模拟或测试。另一方面，TPA迫使你以更能揭示放大器和反馈网络之间相互作用的方式来剖析电路。

开放问题

你更喜欢哪种方法？大学课程是否应该涵盖这两种方法？对这两种方法是应予以同样的重视，还是应舍弃其中一种？如果要舍弃一种方法，会是哪种？欢迎发表意见！

本文转载自电子技术设计。

推荐阅读：

突破开关电源噪声大的魔咒，最强“魔法”在此

动画演示陀螺仪的工作原理，一分钟弄懂

客户投诉器件功耗太大，“元凶”原来是它！

汽车和工业应用中高压侧驱动如何破？图文并茂本文给你正解 

学习路线解析：如何成为嵌入式高手