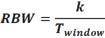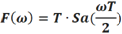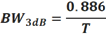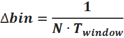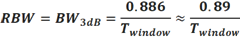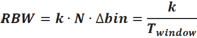快速傅里叶变换(FFT)作为射频电路中一种常用的频谱分析工具,它实现了时域到频域的转换,是数字信号分析中最常用的基本功能之一,FFT也是区分射频技术高低的一个重要分水岭,FFT 频谱分析是否与传统的扫频式频谱仪类似,也具有分辨率带宽(RBW) 的概念?如果具有RBW ,那么FFT 的RBW 又与什么因素有关呢?接下来就给大家一一解答这些疑问。
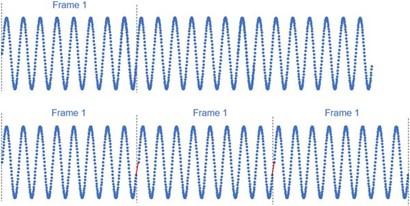
众所周知,FFT 变换是在一定假设下完成的,即认为被处理的信号是周期性的。图1给出了一正弦波信号的采集样点波形,如果对Frame 1作FFT 运算,则会对其进行周期扩展。显然,在周期扩展的时候 ,造成了样点的不连续,样点不连续等同于相位不连续,相当于引入了相位调制,这将导致产生额外的频率成分,该现象称为频谱泄露。
图1. 周期扩展引起样点的不连续
频谱泄露产生了原本信号中并不包含的频率成分,具有诸多危害:首先频率测不准了,通常决定信号频率都是选取幅度最高的谱线,但是幅度最高谱线往往并不是载波,因此造成频率测试结果存在比较明显的偏移,这是调相的影响;其次测得的频谱幅度变小了,本来只有一根谱线,发生频谱泄露后产生众多谱线,但是信号总功率是一定的,因此测得的信号幅度一定会减小;另外,频谱泄露会扰乱测试,尤其在观测小信号时,较强的频谱泄露成分可能淹没比较微弱的信号。
如何避免或者降低频谱泄露呢?这就需要使用下文介绍的时间窗(Window) 技术。
如果能够消除样点不连续,就可以消除频谱泄露。为了实现这一点,需要引入时间窗(Window),时间窗包含的样点数目与信号相同,而且两端的样点值通常为0。在FFT 之前,时间窗与波形相乘,周期扩展后可以保证样点的连续性。
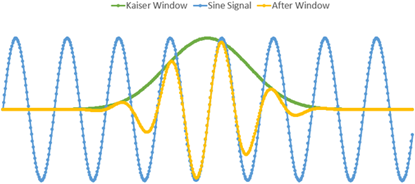
图2以Kaiser Window 为例,给出了时间窗波形、原始波形以及加了时间窗之后的波形。由图可知,引入时间窗后,在周期扩展后并不会造成相位不连续,从而消除频谱泄露效应。
值得一提的是,频谱泄露是无法完全消除的,虽然引入合适的时间窗使得周期扩展后相位连续,但是又等效形成了特殊的射频脉冲信号,所以还会产生一些新的频率成分,只是这些频率成分非常微弱。换句话说,时间窗只能尽量抑制频谱泄露,而无法完全消除!
图2. 引入时间窗以改善频谱泄露效应
在FFT 应用中,时间窗就相当于一个滤波器,不同的时间窗具有不同的频响特性,比如不同的边带抑制和矩形因子等,相应的幅度测试精度也不同。虽然与传统的扫频式频谱仪不同,但是基于FFT 的频谱分析中依然有RBW 的概念,RBW就是指时间窗对应的幅频响应的3dB 带宽,时间窗宽度及类型就决定了RBW 的大小。
RBW 称为分辨率带宽,决定了频谱分析中对多个频率的分辨能力,RBW 越小,分辨率越高。RBW 与时间窗宽度(即Window Time) 成反比,但即使时间窗宽度相同,不同的时间窗类型对应的RBW 也不同,存在一个因子k,并满足如下关系:
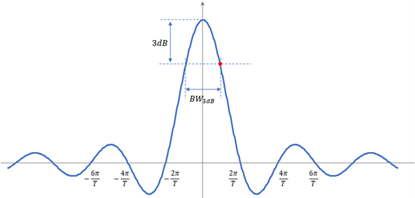
下面以矩形时间窗为例,讨论一下RBW 与时间窗宽度具体有什么关系呢?矩形窗的双边带频谱为Sa(ω) 函数,如图3所示,假设窗口时间为T,则在频率为 ±N*2π/T ( N 为非零正整数) 处均为零点。矩形窗的双边带频谱可以写为如下表达式:
对于图3所示的频谱,相对峰值电平下降3dB的频点位于何处?从电压的角度讲,下降3dB的频点处,幅值降为峰值的 √2/2 。
图3. 矩形窗的频谱特性(双边带频谱)
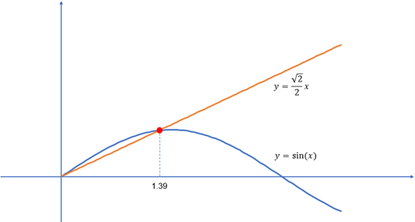
简便起见,利用图4所示的图解法,令sin(x)/x=√2/2 ,则x≈1.39 。经计算ω=2.78/T ,f=ω/2π≈0.443/T 。因此,图3所示的频谱中,3dB带宽为:
图4. x=1.39处,幅值下降3dB
如前所述,FFT 过程中会进行周期扩展,因此FFT 是将信号当作一个周期信号来对待的。FFT得到的频点也是离散的,这些离散的频点称为freq. bin,两个相邻bin 之间的频间距为周期扩展后总时长的倒数。bin 间距决定了频率分辨率,bin 间距越小,频率分辨率越高。假设进行了N次周期扩展,则bin间距为
类似于扫频式频谱分析,FFT 频谱分析中也有RBW 的概念,尽管不存在IF filter 。在FFT 频谱分析中,RBW 决定于时间窗幅频特性的3dB带宽。不同的时间窗类型,具有不同的RBW 表达式。对于矩形窗,RBW 为
从上式可以看出,矩形窗的RBW 并不等于bin 间距,而往往是大于bin 间距。频谱分析应用中通常提及RBW ,但RBW 与bin 间距存在如下关系
式中k为常系数,取决于时间窗的类型。
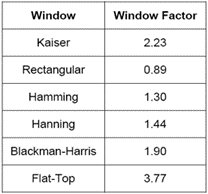
常见的时间窗类型包括:Kaiser、Rectangular、Hamming、Hanning、Blackman-Harris、Flat-Top等。下图给出了不同时间窗类型对应的k因子大小。不同的时间窗,频谱泄露、幅度测试精度及RBW 均不同,测试时应该根据待测信号的特点进行选择。
图5. 不同时间窗类型对应的k因子不同
小结
今天主要给大家介绍了FFT 频谱分析中的RBW 由来,虽然不像扫频式频谱仪那样具有IF filter ,但是FFT 频谱分析中依然存在RBW 的概念。文中以矩形时间窗为例,通过数学的方式解释了RBW 与时间窗宽度的关系。当采用不同的时间窗时,RBW 与时间窗宽度的关系也是不同的,这完全是由时间窗对应的幅频响应决定的。频谱测试时,应当根据测试的信号选择合适的时间窗。